Linear Algebra, Part 6: Matrix Inverses

posted November 16, 2013

In this post we'll look more at matrix inverses and why we care about them.

In the interlude we looked at how we can view an \(m\times n\) matrix as a function which maps vectors in \(\mathbb{R}^n\) to vectors in \(\mathbb{R}^m\). Under that interpretation we saw that bijectivity means invertibility: we can get from any vector in \(\mathbb{R}^m\) back to the original vector in \(\mathbb{R}^n\).

Why do we care about invertibility? The first reason is that with an inverse we can easily solve an equation like \(\A\xx=\bb\) if we have an invertible matrix \(\A\). We find the inverse \(\A^{-1}\) and then just compute \(\A^{-1}\bb\) to get \(\xx\).

The next reason we care about invertibility is that we want to know how to invert matrix composition. If we have a matrix \(\A\BB\CC\), we know that a matrix product \(\A\BB\CC\) is invertible if all of its factors are also invertible: \((\A\BB\CC)^{-1}=\CC^{-1}(\A\BB)^{-1}=\CC^{-1}\BB^{-1}\A^{-1}\).

An example where this matters in practice is from computer graphics: we use matrices to perform geometric transformations such as translations and rotations. Let's start with translation in \(\mathbb{R}^2\): if we want to translate a point \(\pp\) (represented by a vector) by some amount \(a\) in the \(x\) direction and \(b\) in the \(y\) direction, we can construct a translation matrix \(\TT_{a,b}\) and multiply it times \(\pp\) to get a new translated point \(\pp'\).

\[ \pp = \vxy{1}{2} \hskip{0.5in} \pp' = \TT_{2,3}\pp = \vxy{3}{5} \]

Likewise with rotation, we can construct a rotation matrix \(\RR_{\theta}\) to rotate a point \(\pp\) by \(\theta\) radians about the origin:

\[ \pp = \vxy{1}{0} \hskip{0.5in} \pp' = \RR_{\pi}\pp = \vxy{-1}{0} \]

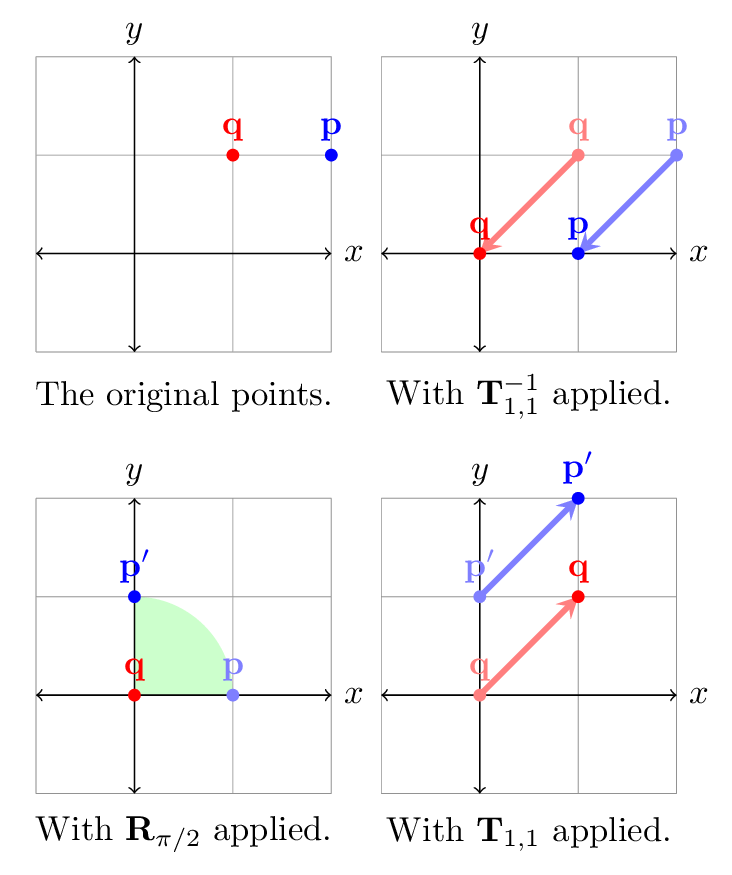
If we want to rotate an object about a specific point \(\qq = \sm{a \\ b}\), we can express this as a product of matrices \(\TT_{a,b}\) and \(\RR_{\theta}\):

\[ \pp' = \TT_{a,b}\RR_{\theta}\TT_{a,b}^{-1}\pp \]

First we use \(\TT_{a,b}^{-1}\) to translate everything so that the point expressed by \((a,b)\) is the origin, then we rotate as desired by applying \(\RR_{\theta}\), and translate everything back to its original location by applying \(\TT_{a,b}\). To do this we need \(\TT_{a,b}\) to be invertible. We might also wish to modularize this transformation as a new matrix \(\A=\TT\RR\TT^{-1}\) and include it in other transformations so we need all of the matrices involved to be invertible.

Here are the inverses of \(\TT_{a,b}\) and \(\RR_{\theta}\):

\[ \begin{align*} \TT_{a,b}^{-1} &= \TT_{-a,-b} \\ \RR_{\theta}^{-1} &= \RR_{-\theta} \end{align*} \]

Some properties of invertible matrices are:

An invertible matrix has only one solution to \(\A\xx=0\), and that solution is the zero vector. This is because the matrix has independent column vectors: no column vector is a combination of any other. If the columns are not independent, then there is some way to combine some of the columns to yield the others. If that is the case, then that combination yields a nonzero solution to \(\A\xx=0\).
Invertible matrices will have a full set of pivots after elimination; non-invertible matrices will have a zero pivot at some point during elimination leading to elimination failure. A missing pivot means we have some unknown with a coefficient of zero which leads to an infinite number of solutions or no solutions for that particular equation.

Afterword

In this post we've seen how we can think of matrix inverses as "undoing" a matrix multiplication and we looked at a few properties of inverse matrices. There are many more; for a full list, see the full Wikipedia article on the subject. For more information on linear transformations such as those indicated by \(\TT_{a,b}\) and \(\RR_{\theta}\), see the Wikipedia article on transformation matrices. Next time we'll look at Gauss-Jordan elimination, a modified elimination process that finds the inverse \(\A^{-1}\) of \(\A\) if it exists.