Linear Algebra, Part 1: Vectors

posted February 14, 2013

Linear algebra is the study of systems of linear equations and vector spaces. I'll be writing a series of posts on this topic as I progress through my study of it. This first post introduces some foundational ideas about vectors.

A vector is a sequence of values. The values in the vector's sequence are called its components. In these blog posts we'll be concerned with vectors with 2 or 3 components.

Notationally, a vector with \(n\) components is represented as an \(n\)-row, one-column matrix. The vector is given a bold single-letter name such as \(\uu\) or \(\vv\). Some example vectors are:

\[ \uu = \vxy 2 7 ~~~~ \vv = \vxyz 1 3 {-2} \]

We refer to the \(i\)th component of a vector \(\uu\) as \(\uu_i\); using the above vectors as examples, \(\uu_2 = 7\) and \(\vv_3 = -2\).

Vector operations

Vectors can be added or subtracted by adding or subtracting their respective elements.

\[ \uu = \vxy 1 7 ~~~~ \vv = \vxy 3 5 ~~~~ \uu - \vv = \vxy {1 - 3} {7 - 5} = \vxy {-2} {2} ~~~~ \uu + \vv = \vxy {1 + 3} {7 + 5} = \vxy {4} {12} \]

In general, for two \(n\)-dimensional vectors \(\uu\) and \(\vv\),

\[ \uu - \vv = \vxyz {\uu_1 - \vv_1} {\vdots} {\uu_n - \vv_n} ~~~~ \uu + \vv = \vxyz {\uu_1 + \vv_1} {\vdots} {\uu_n + \vv_n}. \]

Vectors can be multiplied by a number, called a scalar, which scales the vector's components as well as its magnitude. We write scalar multiplication as, e.g., \(2\vv\).

\[ \vv = \vxy 2 5 ~~~~ 2\vv = \vxy 4 {10} \]

To see how the scalar affects the magnitude, we can work it out in algebra. Given \(\vv = \vxy 2 3\) and some scalar \(c\):

\[ \begin{align*} c\vv &= c \vxy 2 3 \\ &= \vxy {2c} {3c} \\ \|c\vv\| &= \sqrt{(2c)^2 + (3c)^2} \\ &= \sqrt{c^2(2^2 + 3^2)} \\ &= c \sqrt{2^2 + 3^2} \\ &= c\|\vv\|. \end{align*} \]

Geometry of a Single Vector

Typically vectors are represented like the one pictured in Figure 1. Given this geometric representation, a vector can be said to have a direction (which way it points) and a magnitude (its length). The vector's components \(\uu_1\) and \(\uu_2\) correspond to the \(x\) and \(y\) values coinciding with the endpoint of the vector.

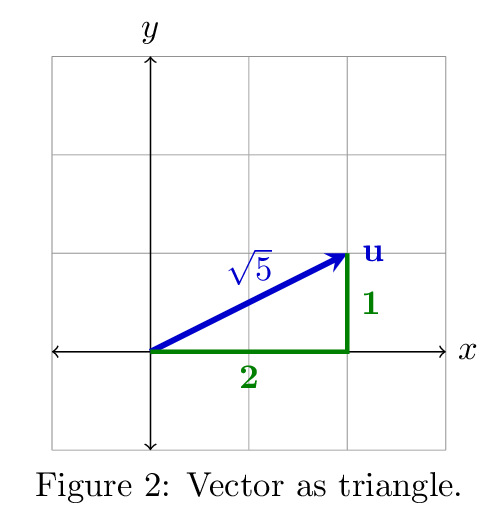
Another way to think about the geometry of vectors is to realize that every vector corresponds to a right triangle (see Figure 2). As a result, we already know the length of the vector from the Pythagorean Theorem. We write this value, the length or magnitude of the vector \(\uu\), as \(\|\uu\|\).

\[ \uu = \vxy 2 1 ~~~~ \|\uu\| = \sqrt{2^2 + 1^2} = \sqrt{5} \]

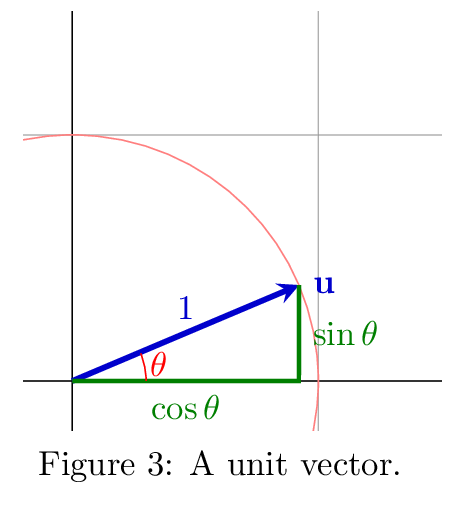
What if the length of some vector \(\uu\) is \(1\)? This is called a unit vector, which I'll write as \(\uuu\) (pronounced "you-hat"). A unit vector can be seen in the radius of the unit circle where it is distanced from the \(x\) axis by some angle \(\theta\) (see Figure 3). Since the vector represents a right triangle, the vector's components are the side lengths. If a radius vector \(\uu\) is \(\theta\) degrees from the \(x\) axis, then we can easily compute the angle \(\theta\):

\[ \uuu = \vxy {\cos \theta} {\sin \theta} ~~~~ \theta = \cos^{-1} \uuu_1. \]

What if the length of a vector \(\uu\) is greater than \(1\)? How can we determine the angle between \(\uu\) and the \(x\) axis? Well, it would be easy to know \(\theta\) if we had a unit vector. To get a unit vector from \(\uu\), we can scale it so that its length is \(1\). To do that, we divide its components by its length:

\[ \uu = \vxy {4} {3} ~~~~ \uuu = \frac{\uu}{\|\uu\|} = \vxy {\frac 4 5} {\frac 3 5} ~~~~ \|\uuu\| = \sqrt{\left(\frac 4 5\right)^2 + \left(\frac 3 5\right)^2} = 1. \]

What happens when we multiply a vector \(\uu\) times a negative scalar, such as \(-2\uu\)? If the scalar is negative, the resulting vector points in exactly the opposite direction (see Figure 4). If the scalar is not equal to \(-1\), the vector's magnitude is scaled, as well.

Geometry of Multiple Vectors

Now we get into something more interesting: the geometric representation of what happens when we add or subtract vectors.

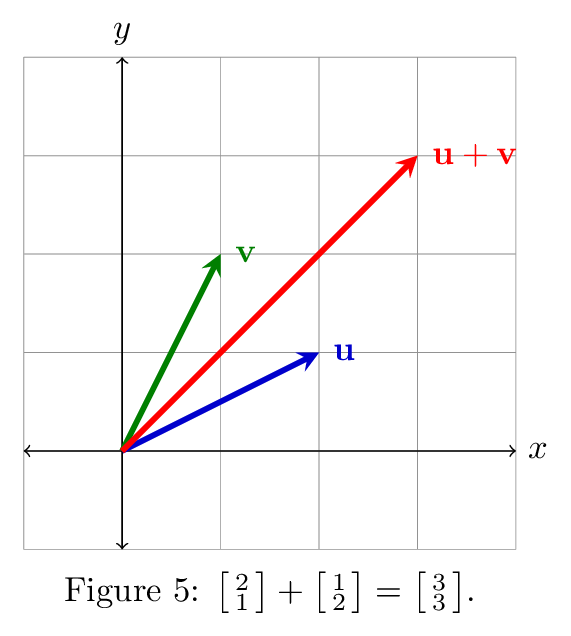
Figure 5 shows an example of two vectors and their sum. The geometry of the sum vector follows from the definition of vector addition: we added the \(x\) components of the vectors to get the new \(x\) component, and similarly for \(y\).

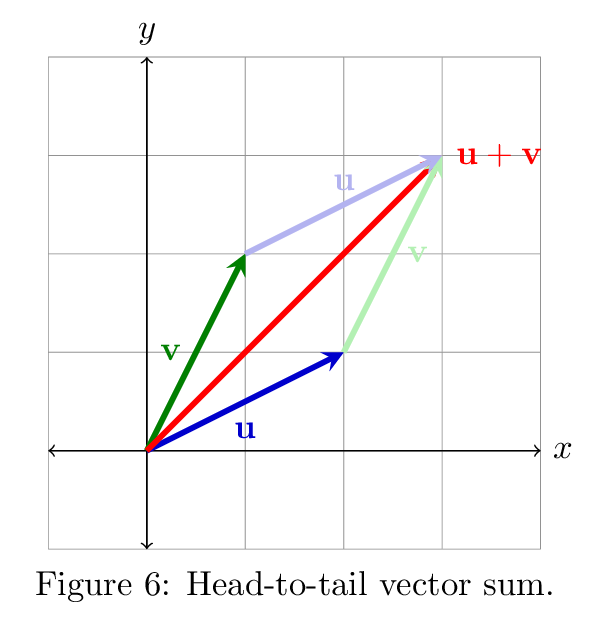
In fact, if we were to attach \(\uu\) and \(\vv\) in a "head-to-tail" fashion so that \(\vv\) starts where \(\uu\) ends, then the resulting "chain" of vectors would end up in the same place as \(\uu + \vv\) (see Figure 6).

Now you can see that the vectors \(\uu\) and \(\vv\) in Figure 6 form a parallelogram. Their sum, \(\uu + \vv\), forms one diagonal of this parallelogram.

The other diagonal of the parallelogram -- connecting the ends of \(\uu\) and \(\vv\) -- is represented by the subtraction of one vector from the other (see Figure 7). Note that we are making a statement only about the length of the difference vector \(\uu - \vv\); it does not originate from the end of \(\vv\), but from the origin as all vectors do. But we present it this way to illustrate its relationship to the other vector operations. The emphasis here is on the relationships between the magnitudes and directions of the various vectors involved.

Up Next

In the next post in this series, I'll cover dot products, the cosine rule, and the Schwarz and Triangle inequalities.